Bilkent University
Mechanical Engineering Department
ACTIVITIES:
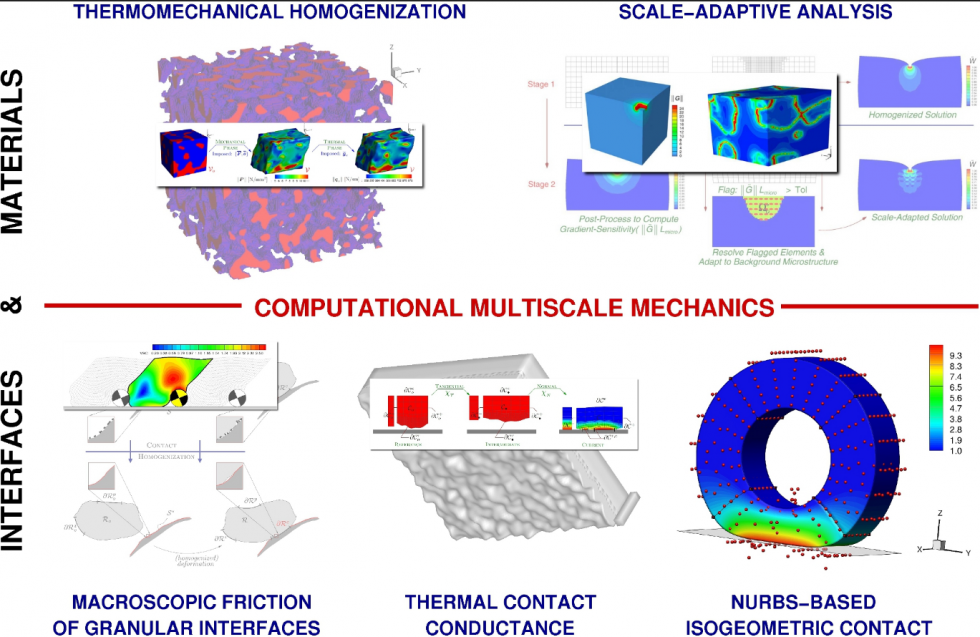
Our research interests lie within the general theoretical and numerical framework of computational mechanics with a special focus on the investigation of problems involving strongly coupled physical phenomena that naturally occur over multiple length and time scales. The ability to convey information across scales is, without doubt, essential for a better understanding of the sources of physical behavior observed on higher scales and helps circumvent the often difficult task of constructing sufficiently accurate phenomenological models to describe these observations. To improve the accuracy and broaden the applicability of robust information transfer schemes, we have been focusing our work along two major research paths, namely the investigation of volumetric and contact homogenization techniques in a fully nonlinear setting for problems involving hierarchical bulk and interface topologies.
Some of the research we have been conducting involves the finite thermoelasticity analysis of heterogeneous media, model reduction through database approaches, simulation of granular interfaces by coupling the Discrete Element Method (DEM) with the Finite Element Method (FEM) as well as the finite thermomechanical and elastohydrodynamic analysis of microrough contact interfaces. Additionally, we develop robust computational contact mechanics algorithms within the isogeometric analysis framework. Links to some of our current projects are provided above.
A central theme in our research activities is the pursuit and development of novel coupling strategies for challenging multiphysics problems. This necessitates a well-balanced combination of theory and computation. Due to the non-standard coupling problems that arise, we have been developing our own simulation packages which are centralized around FEM and DEM.
POSITIONS:
We continuously seek highly motivated MS/PhD students and post-doctoral fellows with proven outstanding academic potential. If you are interested in joining CMML, please contact Prof. Temizer for current positions available.
Students from diverse educational backgrounds such as Civil Engineering or Physics are also encouraged to apply. We always welcome qualified undergraduate students who wish to participate in our ongoing research activities.